Pythagorean Theorem Non Examples

Oleh gibran April 24, 2023 Posting Komentar

By substituting the known sides into Pythagoras Theorem c2a2b2 and letting the height of the wall be a we get. The integer solutions to the Pythagorean Theorem a2 b2 c2 are called Pythagorean Triples which contains three positive integers a b and c.

Proofs By Contradiction

Example 2 solving for a Leg Use the Pythagorean theorem to determine the length of X.

Pythagorean theorem non examples. The Full Pythagorean Theorem Charles Frohman January 1 2010 Abstract This note motivates a version of the generalized pythagorean that says. 32 42 52. 6 2 8 2 10 2.

81 144 216 cos 87 c2. Find the value of x. Solve for the unknown.

Then by square rooting both sides of this equation we get. This is followed by a proof via an elementary computation in exterior algebra. Calculate the value of cos 87.

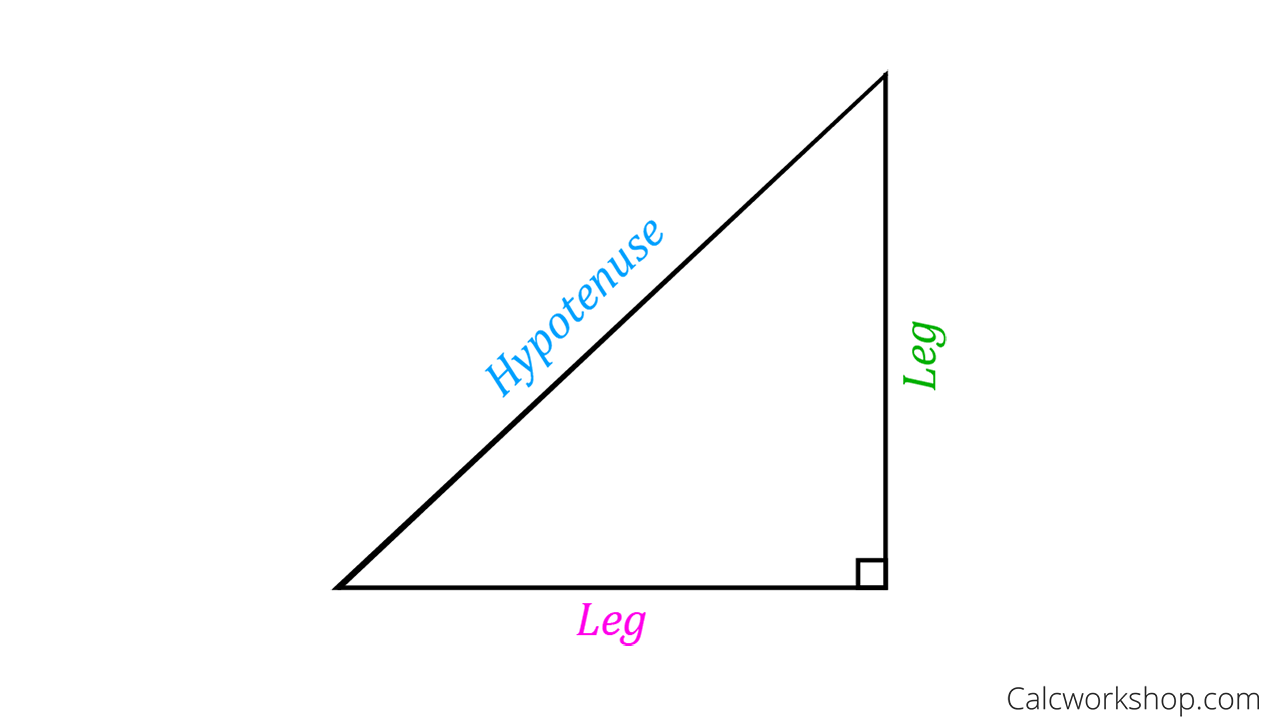
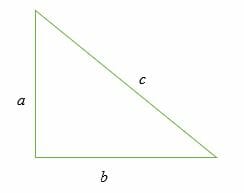
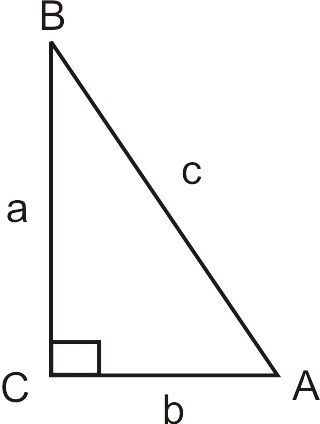
The Pythagorean theorem is unique and true only to triangles with a 90-degree angle. A 2 b 2 c 2. A 2 B 2 X 2 100 X 2 100 X 10 X.

3 4 5 By evaluating we get. If a b and c are the three sides of a right triangle c being the longest side it can be written that a 2 b 2. 6810 326068 16 30 34 etc.

It has been shown in fact to be equivalent to Euclids Parallel Fifth Postulate. Or we could subtract 12 squared from both sides. Thus right triangles in a non-Euclidean geometry do not satisfy the Pythagorean theorem.

Examples for Pythagorean triplets are 3 4 5 5 12 13 7 24 25 8 15 17 9 40 41. For example in spherical geometry all three sides of the right triangle say a b and c bounding an octant of the unit sphere have length equal to π 2 and all its angles are right angles which violates the Pythagorean theorem because. Pythagoras theorem also known as Pythagorean theorem is a quite interesting concept every Maths student would be familiar with the word even non-maths students also would have gone through it in their school time.

The area of the square so formed by arranging the four triangles is c 2. Hence 34 and 5 are the Pythagorean triples. Consider a right triangle given below.

Example for non primitive Pythagorean triples is 6 8 10. Pythagorean theorem intro problems. By Pythagoras Theorem Area of square a Area of square b Area of square c Example.

The equation summarizes the Cosine Law is as follows. The Pythagorean Theorem allows the mathematician to determine the value of the hypotenuse. The Pythagorean theorem in non-Euclidean geometry.

A26 cm 1 dp. 6810 GCF of 6 8 and 10 2. A b are given c is in demand - the script should output that the formula a a b b c c was used in order to compute c.

Calculating the two square roots and rearranging gives us. Were working with triangles and the Pythagorean Theorem right now but I wanted to circle back to the parallel lines angle rules we worked with before Thanksgiving and see how well they could synthesize what they learned. In other words the three sets of positive values in a non-primitive Pythagorean triple are all even numbers.

When my scripts ready it should support more asserts than just the Pythagorean Theorem. 81 144 216 005 c2. So the Pythagorean theorem-- b squared plus 12 squared is equal to 24 squared.

If you dont have a scientific calculator just type cos 87 degrees into Google. The Converse of the Pythagorean Theorem This video discusses the converse of the Pythagorean Theorem and how to use it verify if a triangle is a right triangle. Next in the lesson was an extension of the previous activity by examining special cases of right triangles and Pythagorean triples.

The Pythagorean theorem is derived from the axioms of Euclidean geometry and in fact the Euclidean form of the Pythagorean theorem given above does not hold in non-Euclidean geometry. I can do without a real proof but I really need to know which formulas are used. Created by Sal Khan.

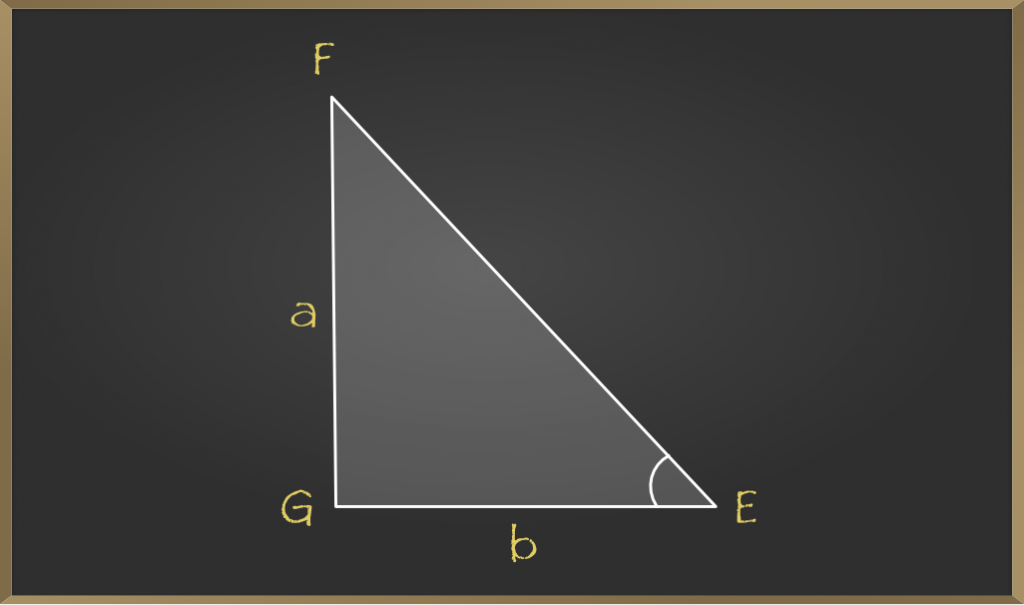
22 Statement of Pythagoras Theorem The famous theorem by Pythagoras deﬁnes the relationship between the three sides of a right triangle. The examples of theorem and based on the statement given for right triangles is given below. A2 B2 C2 2.

This is the currently selected item. The converse of the Pythagorean Theorem manipulates the formula so that the mathematician can use the values to determine that if the triangle is a right triangle. C 2 a 2 b 2 2ab cosC where C is the angle opposite to the hypotenuse.

Both are related to the Pythagorean Theorem. There is one theorem named as Pythagoras Theorem that holds a great importance in our book. This implies a b 2 412 ab c 2 a 2 b 2 2ab 2ab c 2.

A 2 b 2 c 2. Three positive integers a b and c are called Pythagorean triplets if c 2 a 2 b 2 the triple is commonly written a b c ie in increasing order of a b and c. Cos 87 005 to two decimal places.

Here The theorem states that In a right angled triangle the square of the two sides connected to the right angle is equal to the square of the third side called hypotenuse. Now by the theorem we know. If you have a non-right triangle you will have to resort to using the Cosine Law to solve for the missing values.

X is the side opposite to right angle hence it is a hypotenuse. Examples of non-primitive Pythagorean triples include. Insert that new piece of information into the formula.

The area of a square with side a b Area of 4 triangles Area of square with side c. Identify the legs and the hypotenuse of the right triangle. If A is an n k matrix then detAtA X I detA I2 where the sum is over all k k minors of A.

We say b squared is equal to 24 squared minus 12 squared which we know is 144 and that b is equal to the square root of 24 squared minus 12 squared. Pythagorean Theorem says that in a right triangle the sum of the squares of the two right-angle sides will always be the same as the square of the hypotenuse the long side. Overall I think this activity was very effective.

Therefore a 2 b 2 c 2. Intro to the Pythagorean theorem. Sal introduces the famous and super important Pythagorean theorem.

Can I use the Pythagorean theorem with any triangle. The legs have length 24 and X are the legs. Today I started class with students trying to fill in as many angles as they could in the diagram below.

You can say triplets but triples are the favoured term. 36 64 100 100 326068 GCF of 32 60 and 68 4. This activity also had the students do a non-example and show that the Pythagorean Theorem does not hold for non-right triangles.

Also two triangle inequalities used to classify a triangle by the lengths of its sides. The hypotenuse is 26. This theorem gives the fundamental aspect in Euclidean Geometry connecting the.

Converse Of The Pythagorean Theorem Explained 2019